Vítejte v rubrice, která se v jednotlivých volně navazujících příkladech zabývá NC programováním a vším, co s ním souvisí. Postupně, a to zcela od základních kroků, jsou odkrývány elementární problémy, se kterými se lze při obrábění setkat. Například dnes je věnována pozornost zodpovězení otázek formulovaných v minulém čísle tohoto čtrnáctideníku a připojeno je i několik dalších informací.
Předměty zhotovované třískovým obráběním kladou ve všech oblastech použití stále vyšší nároky na přesnost, ergonometrii i estetiku. Vyžadují více a více zaoblené tvary a mimo to – vše musí být vyrobeno rychleji. Téměř veškeré konstrukce se dnes realizují v systémech CAD a pro tvorbu výrobních programů obráběcích strojů, center nebo automatizovaných linek se užívá systémů CAM. Za technologii a výslednou kvalitu však má zodpovědnost do značné míry i specialista u obráběcího stroje. Musí tedy být schopen rozhodování, jaký způsob programování (obrábění jednotlivých součástí) je nejvhodnější.
Metody obrábění se dnes běžně dělí na oblast tzv. klasickou neboli 2,5D obrábění, výrobu ve 3D neboli obrábění ve třech osách a na oblast pětiosého a vysokorychlostního obrábění. Tento výčet není zcela kompletní. Vhodná volba oblasti však musí vždy zajistit dobré ovládání, pohodlné NC programování, optimální výkon v řetězci CADCAM- CNC a v neposlední řadě i maximální možnosti řízení jakosti u stroje. Kupříkladu dnes velmi dynamicky se rozvíjející souvislé obrábění v pěti osách vyžaduje moderní stroje a CAD/CAM softwary. Ty mohou společně zajistit požadavky na výrobu tvarově komplikovaných forem, jakost obrobeného povrchu i rychlost výroby součástí ze zušlechtěných materiálů. Ne každý však běžně vyrábí formy, a tak je mnohdy zcela dostačující využití tzv. obrábění 3 + 2, které může zajistit dostatečnou přesnost výrobku při vyšší tuhosti soustavy stroj-nástroj-obrobek. Navíc je možno ho programovat přímo na obráběcím stroji.
Obrábění tzv. metodou 3 + 2 osy spočívá v NC programování 3 lineárních os (X, Y, Z) a ještě dalších dvou rotačních os. Obecně se rotační osy označují písmeny A, B, C a záleží na kinematice zpravidla frézovacího stroje, která dvojice os je využita (např. X, Y, Z, A, C – koncepce s rotačním stolem; X, Y, Z, B, C – koncepce s rotační hlavou). Prostřednictvím lineárních os se „špička“ nástroje polohuje v pracovním prostoru a kruhovými (rotačními) osami můžeme měnit naklonění nástroje (obrobku). Pomocí 3 lineárních a dvou kruhových os je tedy teoreticky možné napolohovat řezný nástroj do jakéhokoli bodu s požadovanou orientací. Tato metoda (3 + 2 osy) však zpravidla umožňuje pouze změnit polohu obrobku prostřednictvím rotačních os, zafixovat je a následně realizovat souvislé tříosé obrábění (např. vrtání otvoru na šikmé ploše).
S ohledem na výše naznačené rozdílné kinematické uspořádání jednotlivých obráběcích strojů je možno programovat i tzv. směrový vektor. Toho se však zpravidla využívá pouze u souvislého pětiosého obrábění, které je nutno programovat prostřednictvím CAD/CAM softwarů. Popis požadované polohy v NC programu ve vektorovém tvaru je proveden lineárními osami X, Y, Z a orientace nástroje (naklonění) je popsána souřadnicemi A3, B3, C3.
Soustředíme-li se však nyní pouze na základní oblast programování, označovanou jako 2,5D, pak je možno připomenout, že se jedná např. o „klasické“ frézování, při kterém je tvar definovaný dvourozměrnými křivkami obráběn ve směru os X, Y (s konstantním krokem ve směru osy Z). Ve směru osy Z se tedy tvar těchto křivek (tvar součásti) nemění. Do oblasti 2,5D obrábění je velmi často zařazováno např. vrtání otvorů. S tím souvisí i NC programování v tzv. polárním souřadném systému.
Polární souřadnice jsou velmi užitečné např. při NC programování vrtání otvorů na roztečné kružnici nebo např. při frézování n-hranu. Nahlédneme-li na definici, pak je nutno říci, že polární soustava souřadnic je taková soustava v rovině, u které souřadnice označovaná písmenem r udává vzdálenost bodu (řezného nástroje) od počátku souřadnic (pólu) a druhá souřadnice označovaná písmenem ? udává úhel spojnice bodu a počátku od zvolené osy ležící v rovině (nejčastěji jí odpovídá osa X kartézských souřadnic – obr. 1). Obecně řečeno, polární souřadnice jsou vhodné v případech, kdy se při pohybu nemění vzdálenost nástroje od počátku souřadnic (v tomto případě pólu). Transformace polárních souřadnic na kartézské:
x = r . cos ?;
y = r . sin ?.
Transformace kartézských souřadnic na polární:
r = (x2 + y2) ^ (1/2)
? = arctg (y/x)
Tato převodní funkce je však platná pouze na intervalu
? ? <0, ?/2>.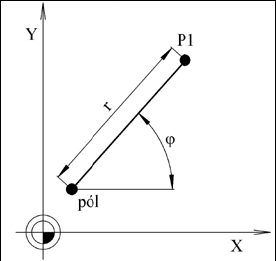
Obr. 1
V minulé kapitole těchto informativních příkladů bylo přibližně formulováno i následující zamyšlení (úkoly): „Přiřaďte jednotlivé osy kartézského souřadného systému k funkcím rovin G17, G18 a G19.“ Stručná odpověď tedy může znít: „Funkce G17 předepisuje práci v rovině XY, funkce G18 předepisuje práci v rovině ZX a funkce G19 je určena pro rovinu YZ (obr. 2).“
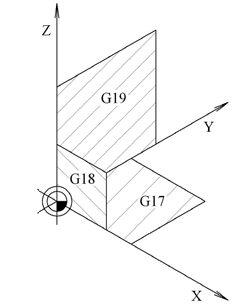
Obr. 2
Směr přísuvu nástroje k těmto rovinám je:
Rovina Směr přísuvu nástroje
XY Z
ZX Y
YZ X
Závěrem je možno ještě dodat, že tzv. pravidlo pravé ruky určuje kladný směr os, odpovídá normě DIN 66217 a zní: Jestliže člověk stojí před strojem tak, aby prostředníček jeho pravé ruky ukazoval proti směru přísuvu hlavního vřetena, potom je přiřazení následující:
- palec ukazuje kladný směr osy X,
- ukazováček ukazuje kladný směr osy Y
- a prostředníček ukazuje kladný směr osy Z.
Článek vznikl za spolupráce Vysokého učení technického v Brně, FSI, ÚST, Odboru technologie obrábění, s firmou Siemens a redakcí Technického týdeníku.
Ing. Aleš Polzer, Ph.D.